Articles

Monarch butterflies and navigation

by Jules Poirier

Millions of monarch butterflies migrate up to 5,000 km each year, but how they navigate is unknown. It is known, however, that because of magnetite in their bodies they could orient themselves by the earth’s magnetic field, but they would still need to use the sun’s position in the sky and know the time of day. This study demonstrates how human navigators could duplicate the migratory achievements of monarch butterflies. The complexity evident in the butterflies indicates that they were created by an intelligent Creator who incorporated amazing design into their navigation system.

The monarch butterfly

The monarch butterfly (Figure 1) has a wingspan of about 10 cm. Its life cycle has four stages. It begins as a 1-mm-diameter egg which its mother glued to the underside of a milkweed leaf. Three days later, a 0.5 mg caterpillar emerges, and feeds on the leaf. It has six simple eyes that can see only black and white. It sheds its outer skin about four times during the first 20 days, a process called moulting. Some 20 days later, the caterpillar has grown about 5 cm long and weighs 1.5 g. It then stops eating milkweed and spins its final silk pad, usually under a protective roof such as a log.

About 12 hours later, when the sun comes up in the morning, the caterpillar jerks in convulsive movements and transforms in 60 seconds to an attractive, 36-goldspotted, 2.5 cm long, green chrysalis. It enters the chrysalis blind, having thrown away its six simple eyes, as well as its sixteen legs and its spinning machine.

In this pupal stage, lasting about eight days, all the caterpillar’s tissues are broken down, and totally rearranged to form the winged adult butterfly. This is a huge problem for evolution. If this process were not fully developed from the start, what selective advantage could the caterpillar gain from having all its tissues breaking down? If the program to develop the butterfly wasn.t fully developed, the insect would have been helpless, and certainly unable to reproduce.

After about eight days the monarch caterpillar transforms into a beautiful monarch butterfly, and comes out of the chrysalis in about 30 to 60 seconds. Its wing veins fill with fluid in 15 minutes, and after drying its wings in the sun for about two hours, it is ready to fly .even as far as 5,000 km to its over-wintering location. During growth of the butterfly, 6,000 lenses for each of its two eyes are built, enabling it to see all the colours of the rainbow, including ultraviolet, as well as the direction of polarisation. All 12,000 lenses were made on the seventh day of the pupal stage. The amazing complexity of the monarch butterfly at each stage of its life cycle is a powerful evidence of the design and variety placed in the creature by an all powerful, intelligent Creator.

The monarch butterfly is the only insect known to migrate annually over long continental distances. It is equipped with a navigational system that can determine its position on the earth and navigate to its migration site as far away as 5,000 km.1,2,3 Monarch butterflies have

been transported 1,500 km off their normal migration course yet, when released, still found their way to their wintering site.4 This paper considers the navigational capabilities required to accomplish a journey of several thousand kilometres. It compares what would be necessary for a human navigator to duplicate the achievement of the monarch butterfly each year as it travels across continent between its summer and winter habitats.

The monarch’s navigational capabilities

It is now recognised that monarch butterflies have navigational capabilities. It is believed they navigate by using the sun’s position or the earth’s magnetic field, or both.

For example, Urquhart states: ‘From these release experiments, I concluded that during the morning period the monarchs moved toward the Sun in search of flowering plants in order to feed. In the afternoon, they flew in their inherent fall migratory direction, toward the southwest.. 5

Williams states:

There is no doubt in my mind that the presence of sunlight is a very important factor in causing certain insects, particularly butterflies, to be active and so migrate.. 6

Gottfried states:

Another of the hypotheses under discussion is that monarchs may use the polarization of the sun’s rays in order to navigate and find the exact latitude and longitude of their over-wintering sites...

He also states:

It has been shown that monarchs possess magnetic material in their bodies, mainly in the head and thorax . . It has been suggested that monarchs use magnetic fields for their navigation.. 7

Brady has made some interesting remarks about animal navigation. He says that ants, bees, homing pigeons and starlings navigate by the sun, stars, or the earth’s magnetic field, or combinations thereof. He states: .It was in 1950, nearly 40 years after Santschi’s original discovery, that time-compensated suncompass orientation was demonstrated simultaneously and independently by Kramer in birds and by von Frisch in bees. ... All these findings clearly established that sun-compass orientation of birds involves compensation for the sun’s motion based on some kind of internal clock regulated by the change of night and day. 8

Perez, Taylor and Jander reported how they had put monarch butterflies in a box away from the sun for periods of time to see if this would change their normal migration direction in a predictable way.9 They concluded that for monarchs in the Northern Hemisphere, for example, time-delayed migrants exhibit a clockwise change in orientation. They followed the released monarchs for about five minutes to determine the monarch’s direction. They also concluded: ‘Monarch butterflies in North America use a Sun compass during their southward autumn migration, orienting their bodies using the time of day and position of the Sun. The monarch butterfly thus joins the small group of species for which a Sun compass orientation mechanism has been demonstrated experimentally. In the absence of celestial cues on overcast days, however, monarchs still manage to orient towards the south-southwest, suggesting that they also have a non-celestial backup mechanism of orientation, such as a geomagnetic compass’. 8

Although the monarchs were disoriented during the first five minutes after they were released from the box away from the sun, it should be noted that they were only tracked for a few minutes. Had they been tracked longer, for a day or so, it may have been found that they eventually determined their exact position and pointed themselves in the correct direction to their over-wintering migration sites. To test this hypothesis, it would be necessary to determine whether the path followed by individual monarchs following their release differed depending on how they were confined prior to their migration journey.

Perez, Taylor and Jander suggest that the monarchs may get disoriented on overcast days because they can’t see the sun, and so may use the earth’s magnetic field to orient themselves.9 This may be true, but it needs to be remembered that monarchs can still locate the sun on overcast days because they can detect the angle of polarisation of the diffuse light.

Street states: ‘The compound eye of the insect and the crustacean is able to detect the angle of polarization, and their brain is then able to work out from this the true position of the Sun..10 He also reports: .But it has been discovered that insects and crustacea are able to navigate accurately by the sun even though it is obscured by clouds, provided that there is at least some blue sky visible’. 11

Chapman 12 has provided much information about insect eyes, such as the colours they can see and how compound eyes can detect the angle of polarisation of the diffuse light.

Monarch butterfly migration

Depending upon the time of year, the monarch butterfly will migrate from the colder latitudes in the fall to over-wintering sites at warmer latitudes. In the spring, the monarchs return to where they were born. On the North-American continent, the monarch populations that live west of the Rocky Mountains overwinter in California and Mexico. Those populations that live on the east of the Rocky Mountains over-winter in Florida, Bermuda, the Bahamas and Mexico. Butterflies living around Ottawa, Canada, are known to migrate to the region of Morelia, Mexico. 1 Almost all of the workers previously cited agree that monarch butterflies navigate using the sun’s position with perhaps the aid of the earth’s magnetic field. However, not one worker considers what detailed information about the sun’s position and the earth’s magnetic field would be needed by the butterfly to determine its location. This paper addresses that question.

We will consider what would be involved for a navigate 3,600 km to Morelia, Mexico. We will explore how human navigators would tackle the problem. How could human navigators determine their location on the earth? How could they know which direction to travel to reach the over-wintering site in Mexico where they had never been? From a knowledge of the sun’s position at different dates and of the earth’s magnetic field, human navigators could determine their co-ordinates as follows:

(1) Latitude (degrees north or south of the equator) from knowing the sun’s position at a given time and date and comparing these with current astronomical data such as the Navigator’s Almanac.

(2) Longitude (degrees east or west of Greenwich, England) either by measuring differential sunrise time and comparing this with an astronomical almanac or by measuring the direction to the earth’s magnetic pole, with a magnetic compass, and comparing this with true north.

By comparing with human navigation, therefore, I would like to demonstrate how the remarkable migration achievements of monarch butterflies point to their amazing navigational ability.

Required navigational capabilities

If our human navigators are to faithfully re-trace the migratory route of the monarch butterflies, then their navigational instruments must be consistent with what could plausibly be employed by the butterfly. What would be the minimum capability needed by human navigators to migrate great continental distances successfully? As a minimum requirement, our human navigators would need:

1. A clock that can be set to zero time (T0) and then stopped at a later time (T1), whenever they desire. That is, the navigators need a basic stopwatch that can also be used as a 24-hour clock.

2. The ability to measure angles from their horizon to the height of the sun’s position. The sextant is the well-known angle-measuring instrument widely used by humans for navigation.

3. The ability to measure angles along the horizon from the sun’s sunrise position to any desired direction.

4. A magnetic compass that always points in the direction of the earth’s magnetic pole. Monarch butterflies have magnetite in their bodies and so are able to orient themselves with respect to the earth’s magnetic field. 1

5. Sufficient astronomical information of the sun’s position while traveling on their intended migration path from Canada, to Mexico. For human navigators this information can be obtained from an astronomical almanac, but the data could be reduced to simplify the navigation process. How would navigators who had these capabilities determine their location on the earth? Assume one morning, for example, some human navigators awoke in a strange land and did not know where they were. All they possess is a magnetic compass, a sextant, a clock and a current astronomical almanac. Unlike most human navigators, they do not have a second clock, that can tell the time at 0 ° longitude through Greenwich, England.

The following steps show how these navigators could determine their position on the earth. Let us assume they are located near Ottawa, Canada, at latitude of 45 °N and longitude 75 °W, but do not yet know their location . Being determined to establish where they are, they await the rising of the sun on the next morning to locate themselves. Here is how they would determine their latitude.

Determining latitude

The next morning the navigators must set their clock time to zero at the time the sun rises (T0). Then they would start measuring the angle from their horizon to the height (H) of the sun’s position. The sun’s maximum height angle (Hm . say 49.3 °), which occurs at midday, and the midday time (Tm . say 6.39 hours) are recorded. The navigators know that the length of the daylight will be twice this midday time, (2 x 6.39 = 12.78 hours), but to be sure, they allow the clock to continue running until the sun sets. At sunset, the navigators stop their clock and check that the length of daylight time (Td) equals 12.78 hours. From this length of daytime (Td) and the maximum height angle (Hm), the navigators can determine their unique latitude and calendar date, provided they have access to appropriate astronomical information.

Figure 2 shows the geometrical relationship between the navigators, the sun’s path in the sky, the sun’s maximum height angle, and day length for September 11, 1992 at a latitude of 45 °N. At this latitude, on this day, t he sun’s maximum height angle (Hm) would be 49.3 ° occurring at a midday time of 6.39 hours. Note that there are other dates when the maximum height angle (Hm) can equal 49.3 °, but the length of daylight time (Td) would be different. The navigators must therefore know both the sun’s maximum height angle (Hm) and length of daylight time (Td) to be able to tell their latitude and calendar date.

Figure 3 shows the sun’s maximum height angle (Hm) for the dates September 1 to 22, 1992. The maximum height angles (Hm) were calculated using the following equation: Hm = 90 - L + d where L = latitude of the observer (in degrees) d = declination angle of the sun’s position at midday (in degrees) for a given date and latitude. The declination angle sign is (+) for north declinations and (-) for south declinations.

Figure 4 shows the relationship between the latitude (L), the declination angle (d) and the maximum height angle (Hm) for three days and three latitudes. Figure 4(a) shows the angles for September 11, 1992 at a latitude of 45.0 °N and declination of 4.35 °N. Here

Hm equals 49.35 ° (90.0 - 45.0 + 4.35). Figure 4(b) sh ows the angles for November 5, 1992 at a latitude of 30.8 °N, and declination of 1 5.83 °S. Here H m equals 43.37 ° (90.0 - 30.8 - 15.83). Figure 4(c) shows the angles for June 21, 1992 at a latitude of 20.0 °N and declination of 23.43 °N. Here H m equals 93.43 ° (90.0 .20.0 + 23.43), or looking northward, Hm would equal 180.0 - 93.43 = 86.57°. Therefore, after awaking in a strange land from a long sleep, our navigators would be able to determine their latitude and the calendar date. They would need to carefully observe the sun’s maximum height angle (Hm) as it traveled though the sky, and the length of the day between sunrise and sunset (Td). They would also need to refer to relevant astronomical information as contained in an astronomical almanac.

Determining longitude from differential sunrise time (TRS)

Our navigators, after awakening from their long sleep, have determined their latitude to be 45 °N, and the date to be September 11, 1992. Ho wever, they will need to determine their longitude (how far west or east of a given location) once their migration begins.

Once preparations are complete, their starting date for migration is set at October 1, 1992. On this day, our navigators set their clock at sunrise to 5.96 am, because they know from the almanac that at their latitude of 45 °N the sun will rise at that time on October 1, 1992. Now, as the navigators travel their south-west journey, their clock will read four minutes later in time for each degree west of the original starting longitude of 75 °W, or one hour later for each 15 ° west of thei r starting longitude. For example, if on October 30 their clock sunrise time reads 7.27 am, they would know from their almanac that at their new latitude of 33.3 °N the sunrise t ime at this new location would be 6.27 am. The differential sunrise time (TRS) is therefore 7.27 . 6.27 = 1 hour. Their new longitude is then 75 °W + [(7.27 . 6.27) x 15 °W] = 90 °W, that is, 15 ° west of their starting longitude.

Therefore, once on their journey, our navigators could determine their relative longitude from the differential sunrise time (TRS), but they would also need to refer to relevant astronomical information as contained in an almanac.

Determining longitude from the earth’s magnetic field

Alternatively, our navigators could determine their longitude by knowing the direction to the earth’s magnetic pole and true north. The earth’s north magnetic pole is not at the same location as the true north pole. Furthermore, the annual rate of change is about 2 arcminutes west (that is, the magnetic declination is decreasing by about 2 arcminutes per year). For the purpose of this paper, we will assume the north magnetic pole is located at latitude 73 °N and longitude 102 °W. Re call that the north pole is located at latitude 90 °N, and all longitudinal meridians go t hrough the north pole. If the magnetic north pole were at the true north pole, all magnetic compass needles would point in the direction of true north no matter what longitude the pole is not at the true north pole, compass needles do not point to the true north. The error angle (E) between the direction to true north and the direction to magnetic north changes with longitude.

Navigators can therefore determine their longitude by measuring this error angle (E). For example, using our assumed magnetic north pole location, at a starting latitude of 45 °N and longitude of 75 °W, the error angle (E) is 14 ° west of true north. At a longitude of 60 °W, the error angle (E) would be 21 ° west from true north.

Figure 5 shows the magnetic compass error angle (E) for three longitudes at a latitude of 45 °N, and Figure 6 shows the magnetic compass erro r angles (E) at latitudes 45 °N and 30 °N for longitudes between 60 °W and 120 °W. Note that the error angles are less at tude 30 °N than at 45 °N for the same longitude . However, the error angles are sufficiently large and different at the lower latitude to determine longitude. For example, the error angle (E) is only 12 ° for 75 °W and lati tude of 30 °N, but the error angle (E) is at a latitude of 45 °N for the same longitude of 75 °W. Note also that the error angle (E) is zero at the west longitude of 102 °W because the compass direction is the same as the direction to true north.

Maps that show the error angle (E) at different locations on the globe (magnetic declination maps) are published regularly by such organisation as the US Geodetic Survey. Also, they generally show the annual rates of change. Why the magnetic north pole changes its location with time is unknown, but it is believed to result from the earth’s rotation acting upon the mechanism that generates the magnetic field in the core.

The error angles in Figure 6 were determined from published magnetic declination maps and by measurements made on a 25 cm diameter globe of the earth. Therefore these angles would not be as accurate as those obtainable from the U.S. Geodetic Survey magnetic isogonic maps.

The next question faced by our navigators, as they seek to determine their longitude, is how to measure the magnetic error angle if the direction to true north is not known. The magnetic compass points to the magnetic north pole, but what is the direction to the true north pole?

The direction to the true north pole can be found by measuring the horizontal azimuth angle (A) from the sun’s position at the time of sunrise to the direction of true north. This azimuth angle (A), measured at sunrise, varies with latitude and date. Figure 7 shows ow the azimuth angles vary between October 1 to November 29, 1992 at latitudes from 20 °N to 45 °N. For example, this figure indicates the azimuth angle on November 11, 1992 at 28.3 °N latitude to be 110 °. This is measu red from true north (0 °) to the position of the rising sun. Therefore, to obtain the direction to true north on November 11, 1992 and latitude 28.3 °N, the navigators would , after facing the sun at sunrise, turn 110 ° left (counter clockwise). They would then be facing true north.

Consequently, as an alternative to the sun, it would be possible for our navigators to determine their longitude by measuring the error angle (E) between magnetic north and true north. Besides the ability to detect the earth’s magnetic field, and to measure the angle of the sun, they would also need to have access to information that relates the magnetic error angle to different locations on the earth. The direction of magnetic north could be determined from their compass, but the direction to true north would need to be determined from the sun’s position at sunrise. By knowing this direction together with the latitude and date, the direction of true north can be determined. The navigators would also need to refer to relevant astronomical information from an almanac.

Planning the 3,600 km journey

Now that our navigators can determine latitude and longitude, let us assume they plan to fly from Ottawa, Canada (45 °N, 75 °W) to the city of Morelia, Mexico (20 °N, 100 °W).

This is one typical route for monarch butterflies east of the Rocky Mountains. Attaching one earth, and the other end on the final location, the navigators determine the distance at 3,600 km. This distance is the shortest path length possible, and is called a great circle path. Let us assume they plan to complete the trip in 60 days, starting out on October 1, 1992 and arriving at their final destination on November 29, 1992. They determine the latitude and longitude for ten equal 360 km distances along the path.

From the navigational techniques previously described, the required navigational data for each of the eleven locations can be determined.

Table 1 shows the ten navigational data needed for eleven, equidistant locations along the proposed journey. To accomplish this proposed path a monarch butterfly would have to travel 3,600 km in 60 days, or 60 km per day. Assuming the monarch butterfly travels for six hours each day, its average speed would need to be 60/6 = 10 km per hour. Since a monarch butterfly can fly up to 50 km/h without assistance from the wind, 3 this travel plan seems very feasible.

From the data in Table 1, our navigators can determine their latitude along the path by measuring the sun’s maximum height (Hm) each midday. The sun’s maximum height (Hm) should be increasing as each day progresses, starting at 41.6 ° on October 1, 1992 and measuring 48.4 ° on November 29, 1992. The (H m) angles along the proposed journey are graphed in Figure 8.

If, on any given day, the maximum height angle (Hm) is greater than shown in Table 1 or Figure 8, the navigators know they are farther south than they planned to be. If, however, their height angle (Hm) is less than that shown, the navigators know they are further north than they should be and must increase southward travel time the next day.

There are two ways navigators can use the data in Table 1 to determine their longitude along their path. First, they can note what the magnetic compass error angle (E) should be at each sunrise time. If the error angle (E) is more than what it should be for each location, their longitude is less than it should be or they are east of their desired location.

For example, assume on October 18 the navigators measure the error angle to be west 10 °. From the data listed in Table 1 the error ang le should be 9.8 °, so the navigators know they are east of where they should be. Figure 9 shows the error angle (E) needed for the proposed journey.

Second, they can determine longitude from the differential sunrise time (TRS).that is the clock sunrise time at their new location minus the almanac’s sunrise time for the same location. At their starting location (45 °N, 75 °W) on October 1, 1992 the navigators’ clocks were set at sunrise to 5.96 am. The differential sunrise times (TRS’s) for the proposed journey are listed in Table 1 in minutes and shown graphically in Figure 10. As each day progresses, the navigators can read their TRS’ and for each four minutes of TRS can know that they have traveled one degree of longitude from the starting longitude. Note that for each of the eleven equidistant locations, the TRS increases from zero minutes to a maximum of 100 minutes at the final destination. If at a given location, the differential sunrise time (TRS) is greater than shown in Table 1, the navigators know they have traveled too far west of their desired path. If the TRS is less than shown in Table 1, then the navigators have traveled too far east of their desired path. Thus the navigators. clock time identifies the west or east error at each sunrise time.

The course angles (C) in degrees shown in Table 1 were obtained from a 25 cm diameter globe of the earth along the path for ten equal 360-km distances. More accurate course angles can be calculated from spherical trigonometry, but the navigators would not have to calculate them because the course angles could be supplied as a look-up table. The course angle (C) is measured from the direction to true north clockwise to the direction the navigators must take to follow their path to their destination. For example at the starting point in Ottawa, Canada, on October 1, 1992, the course angle (C) is 228 ° pointing the navigato rs along the great circle path to Morelia, Mexico. Figure 11 shows the course angles needed to follow the planned path for the proposed journey.

By traveling along on a great circle between their winter and summer habitats, the butterflies would minimise energy consumption. However, navigating along a great circle calls for continuous adjustment of the course angle. This would make navigation an achievement even more complex than using just eleven points as described in this paper. These navigational abilities strongly support the concept of design input into the insect from an intelligent Creator.

Monarch navigational capabilities

If, as suggested by the workers cited, butterfly navigation is based primarily on the position of the sun, then a minimum level of instrumentation is required. This includes the ability to accurately track the time of day, and the ability to measure the angular position of the sun both vertically and horizontally. In addition, the butterfly would require astronomical information about the path of the sun at different latitudes and different times of year. If, as is also proposed, the monarch butterfly uses the earth’s magnetic field for navigation, then, in addition, it would need the ability to measure the direction of the earth’s magnetic field together with information about how the field varies with latitude and longitude.

The monarch butterfly could accurately measure the sun’s position in the sky with respect to other geographical features using its two amazing 6,000-lens compound eyes.

With this instrument, several different objects could be viewed at the same time and the relative angular positions determined. How a monarch butterfly could track time is less understood, but there are many complex biological clocks in organisms that suggest ways that this could be done. Even the detection of the earth’s magnetic field is considered feasible because it is known that the monarch butterfly has magnetite in its body which would permit such measurements and allow it to position itself accordingly.

However, much less is understood about how the monarch butterfly could obtain information about the sun’s position at different geographical locations at different times of the year, or information on the direction of the earth’s magnetic field in different parts of a continent. Furthermore, how this information could be passed from one generation to the other is wholly unknown.

The ability to navigate alone does not constitute the ability to successfully complete a migratory journey. Navigation needs to be complemented by the ability to plan the expedition. Not only is navigational information about the destination required, but also

information on the intermediate positions along the way. How this data is determined and stored by the monarch butterfly is a mystery. Even more amazing is how this information could be passed from generation to generation. Perhaps the butterfly utilizes navigational techniques different from those which humans would use to accomplish the same feat.

Some of the many mysteries surrounding monarch butterfly navigation could be explored by housing some monarch butterflies in a large cage inside a room illuminated with a single light. The size, intensity and position of the light could be varied continuously to simulate the path of the sun in the sky during the day. In different experiments the path orientation, and duration of the ‘sun’ could be changed to simulate different locations on the earth. Furthermore, the orientation of the path of the .sun. could be varied with respect to the earth’s magnetic field. By monitoring the behaviour of the monarch butterflies under these conditions, we could determine whether there is a preferred flight orientation and whether this corresponds to the direction required for their migratory journey. Furthermore, the response would also indicate whether butterfly navigation depends primarily on the sun or on the earth’s magnetic field.

Conclusions

It would be extremely difficult for humans to duplicate the navigational achievements of monarch butterflies. Human navigators would require a clock, a sextant, a current astronomical almanac, a compass, and a current magnetic map of the region. Even with these instruments, they would require a high level of observational skill and computational ability to travel some 3600 km across a continent between specific locations.

With these instruments, human navigators could determine their latitude by measuring the sun’s maximum height angle (Hm) at midday and the length of daylight time (Td). By comparing their measured (Hm) and (Td) with values in their astronomical almanac, the navigators could determine their latitude and calendar date. Navigators could determine their longitude east or west of their starting longitude by measuring the differential sunrise time (TSR) at each new position along their journey. Alternatively, human navigators could determine their longitude by measuring the error angle (E) between magnetic north and true north.

It is possible that the monarch butterfly could accurately measure the sun’s position in the sky with respect to other geographical features using its two amazing 6,000-lens compound eyes. Furthermore, the butterfly may be able to accurately keep track of the time with a biological clock similar to those in other organisms. Detection of the earth’s magnetic field is feasible because the monarch butterfly has magnetite in its body by which it could position itself accordingly.

However, little is understood about how the monarch butterfly could have access to information about the sun’s position at different geographical locations at different times of the year, or information on the direction of the earth’s magnetic field in different parts of a continent. Nor is it known how a butterfly could ‘plan’ its journey to obtain the navigational information about its destination and its intermediate positions along the way. Even more amazing is how the necessary navigational data base could be passed from generation to generation.

The sheer complexity of the navigational task suggests that the monarch butterfly uses navigational techniques different from those which humans would use to accomplish the same feat. Experimental work is necessary to help resolve what navigational methods are used by the butterfly to accomplish its long migration.

Only the Creator knows how monarch butterflies navigate, but we have shown how difficult it would be for human navigators equipped with very basic measuring instruments to determine their position on the earth. How the Creator implements these complex features into the design of the monarch butterfly is unknown. Such a result could not have come about by random chance.

Fig. 1 is a monarch

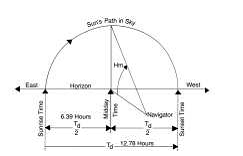
Figure 2. The relationship between the sun.s maximum height angle (Hm), the length of day (Td) and the sun.s path in the sky. For September 11, 1992, H m equals 49.3° and T d equals 12.78 hours.


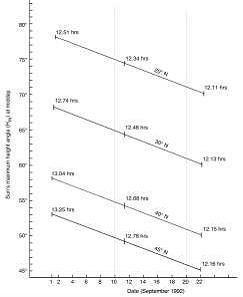
Figure 3. The sun's maximum height angle (Hm ) for September 1 to 22, 1992, between latitudes 20°N and 45°N. The length of the day (Td) is shown in hours for 1st, 11th, and 22nd of the month.

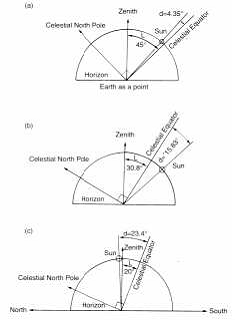
Figure 4. The relationship between latitude (L), declination angle (d), and the sun.s maximum height angle (H m).
a) L = 45°N on September 11, 1992.
b) L = 30.8°N on November 5, 1992.
c) L = 20°N on June 21, 1992.

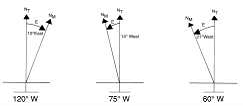
Figure 5. Magnetic compass error angle (E) for three longitudes at latitude 45°N. NT is true north and NM is magnetic north.


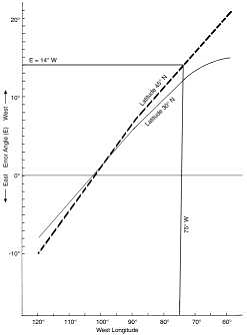
Figure 6. Variation of magnetic compass error angle (E) with longitude for two latitudes over the North American continent.

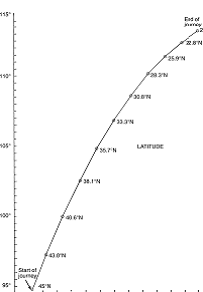
Figure 7. Azimuth angle (measured clockwise horizontally from true north) to position of the sun at sunrise at various dates along hypothetical journey from Ottawa, Canada (45°N, 75°W), starting on October 1, 1992, and ending at Morelia, Mexico (20°N, 100°W), on November 29, 1992.

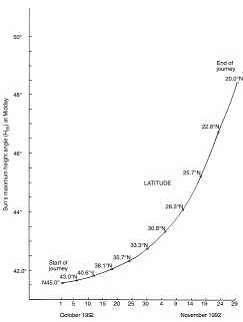
Figure 8. Sun.s maximum height angle (Hm) along hypothetical journey from Ottawa, Canada (45 °N, 75 °W), startin g on October 1, 1992, and ending at Morelia, Mexico (20°N, 100°W), on November 29, 1992.

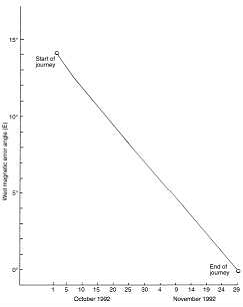
Figure 9. Magnetic error angle (E) along hypothetical journey from Ottawa , Canada (45°N, 75°W), starting on October 1, 1992, and ending at Morelia, Mexico (20°N, 100°W), on November 29, 1992.

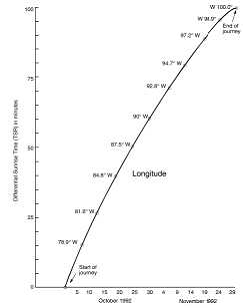
Figure 10. Differential sunrise time (TRS) along hypothetical journey from Ottawa, Canada (45°N, 75°W), startin g on October 1, 1992, and ending at Morelia, Mexico (20°N, 100°W), on November 29, 1992.

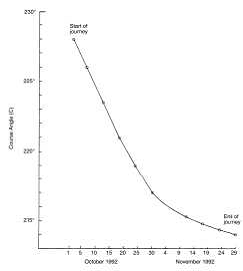
Figure 11. Course angle (C) required to navigate along hypothetical journey from Ottawa, Canada (45°N, 75°W), starting on October 1, 1992, and ending at Morelia, Mexico (20°N, 100°W) , on November 29, 1992.

See website for Table 1.

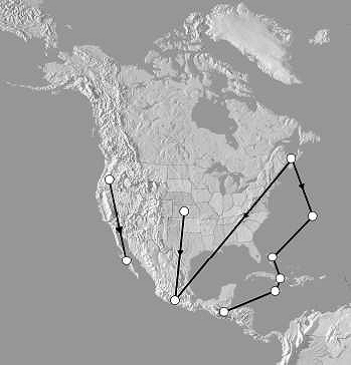
The monarch butterfly is the only insect known to migrate annually over major continental distances. It is intriguing to note that there are other monarchs in other parts of the world that do not migrate's

References

1. Poirer, J., 1995. From Darkness to Light to Flight, Institute for Creation Research, El Cajon, California, has more details

about the life cycle of the monarch butterfly and its fantastic navigational capabilities.

2. Poirer, J., 1998. The Life and Adventure of Monica the Monarch, Master Books, Green Forest, Arkinsaw, is a children.s

book that tells the life story of a female monarch butterfly from her point of view.

3. Poirer, J., 1998. The magnificent migrating monarch, Creation Ex Nihilo, 20(1):28-31.

4. Urquhart, F., 1987. The Monarch Butterfly . International Traveller, Nelson Hall, Chicago, p. 153, describes these

miraculous, complex, navigational feats of the monarch butterfly.

5. Urquhart, Ref. 3, p. 148.

6. Williams, C.B., 1958. Insect Migration, Collins, London, p. 126.

7. Gottfried, C. 1990. One of Nature.s Most Incredible Phenomena; The monarch butterflies. In: Proceedings of the Royal Institution of Great Britain, Vol. 62, p. 143.

8. Brady, J., 1982. Biological Timekeeping, Cambridge University Press, UK, pp. 49.53.

9. Perez, S.M., Taylor, O.R. and Jander, R., 1997. A sun compass in monarch butterflies. Nature, 387(6628):29.

10. Street, P. 1976. Animal Migration and Navigation, Brunel House, London, p. 102.

11. Street, Ref. 9, p. 101.

12. Chapman, R.F., 1982. The Insects . Structure and Function, Harvard University Press, Cambridge

The monarch butterfly is the only insect known to migrate annually over major continental distances.

It is intriguing to note that there are other monarchs in other parts of the world that do not migrate.

Jules Poirier has a Bachelor of Applied Science degree from the University of California, Berkley and is a retired Senior Design Specialist Electronic Engineer. Involved for many years in designing circuitry for a range of navigational equipment, including the Saturn radar pulse altimeter, Mr Poirier, after his retirement, became interested in the complex navigational ability of the monarch butterfly. He has spent many hours researching this amazing creature and its navigational equipment.

http://www.creationontheweb.com/images/pdfs/tj/tjv13n1_butterflies.pd

Used by permission of Creation Ministries International: www.creationontheweb.com